全文收录于 专辑《白话高中数学》，同时收录于《白话详解高考数学十年真题（函数和导数）》点击可以阅读合集全部文章

026（2017课标全国卷2理数第21题 ）

解析：本题主要考察经典不等式的运用,二阶导求解隐零点范围问题

预备知识：有如下经典不等式存在：

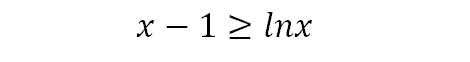
图形是这样的：

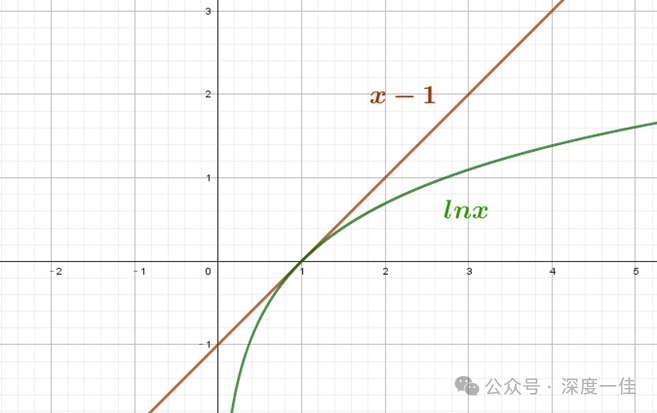
只需要把左右两边作差，然后判断作差函数的单调性，求出最小值，就可以证明上述不等式。

这个不等式有几个变式，比如：

把上述图形在x轴向左平移一个单位，不等式就变成：

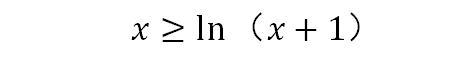
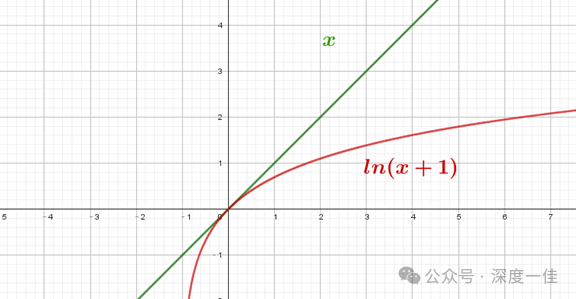
同理，把第一个图形在y方向上向上平移一个单位，不等式就变成：

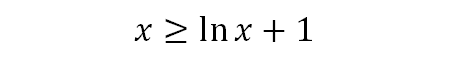
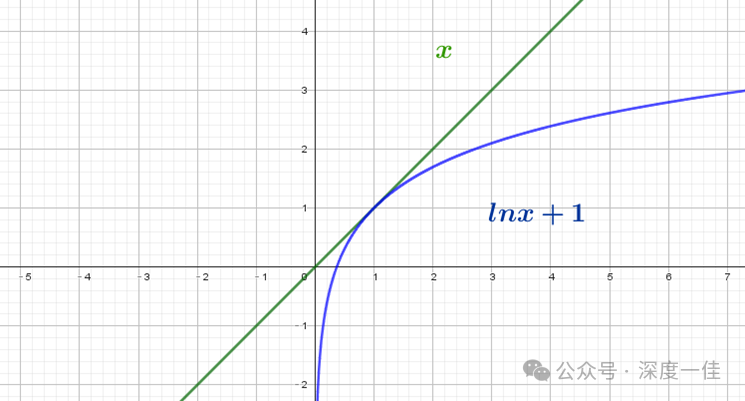
把第一个不等式左右两边同乘以一个正数x，又可以获得另外一个变式：

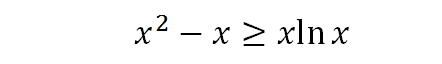
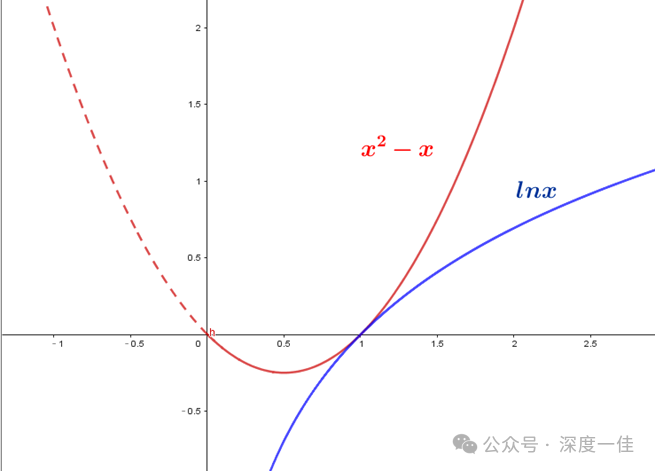
这个经典不等式和它的几个变式，图像都比较直观，很容易获得清晰的记忆。作为工具储备，需要用的时候，直接调用记忆的图形，准确性比记忆代数式要靠谱。

说完了预备知识，开始本题的解析：

(1)函数f(x)定义域x∈（0，+∞），但函数值不小于0，注意这种不小于0的描述，因为定义域是开区间，端点值都不是确定值，因此可以肯定，函数在定义域内是有增有减的，且最小值不小于0。

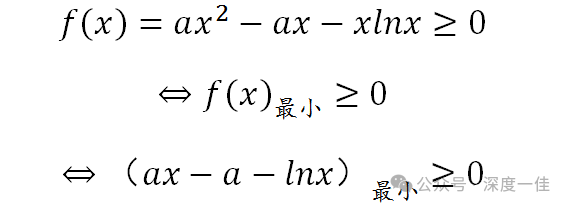
为什么这里将原函数不等式两边同除以一个x?,无它，因为x∈（0，+∞），两边同除x不影响不等式的运算，而且还可以把需要运算的代数式化简。

触及灵魂的问题接着就来了：既然不影响运算，为啥要化简呢？

因为学数学的人都懒的要命，心理偏执到不最简就会浑身不舒服的程度。

要不，你原函数直接求导尝试一下，你会发现，求极值点的时候，题目就会做不下去，直接给你难堪。

所以，学数学谨记一个心法口诀：代数运算中，只要能化简的，想都不用想，直接化简就完了。

好，现在我们只需要保证这个化简后的新函数最小值不小于0就行了。

下一步就是求导观察这个新函数的单调性，找到极值点：

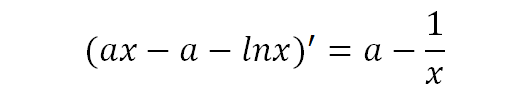
令这个导函数为0.可以求出极值点：

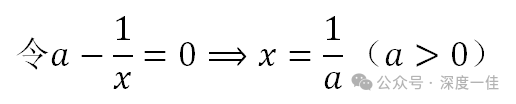
极值点左侧，导函数值小于0，新函数单调减，右侧，新函数单调增，等于1/a时，新函数取得最小值：

只要让这个最小值不小于0，就能保证原函数不小于0，所以只需：

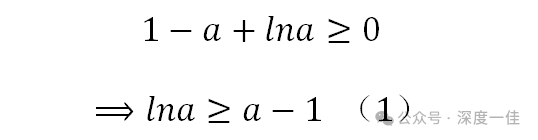
到这里开始用到预备知识中的经典不等式，经典不等式告诉我们：

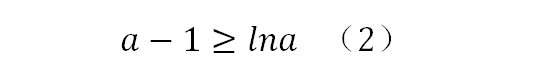
既要保证（1），又要满足（2），那就只能取它们的交集：

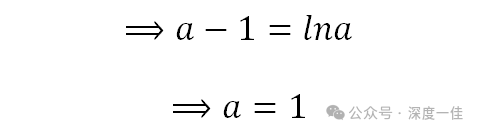
2） 根据a的结果，原函数为：

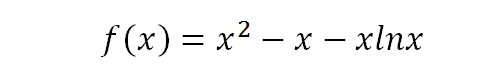
要证明：1、存在唯一的极大值点，仅此一家，绝无分号；

2、这个唯一的极大值在两个具体的实数值之间。

首先解决第一个问题，证明函数存在极大值点，而且是唯一的。

求导是第一要务：

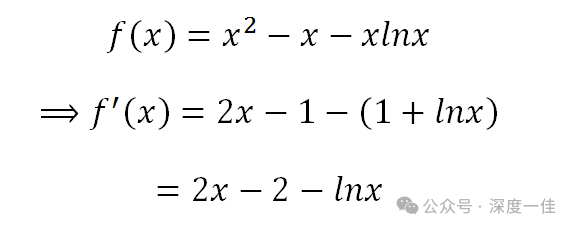
我们令导函数为0：

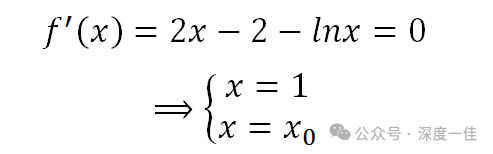
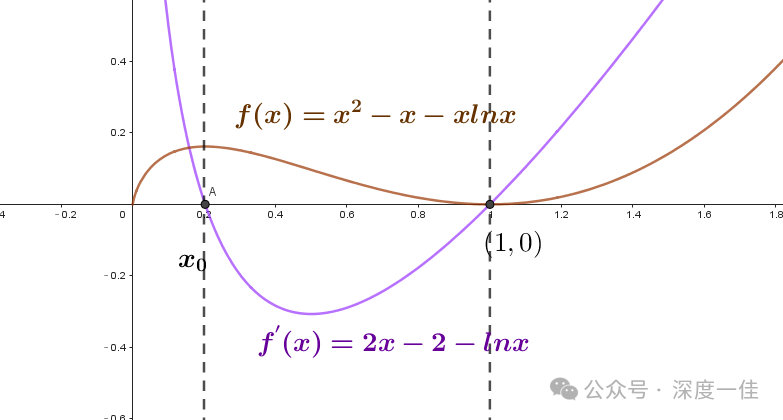
很明显，这又是一个超越方程，我们没有办法把另一个解用确定的实数表示，但我们可以通过作图，找到它的大致范围：

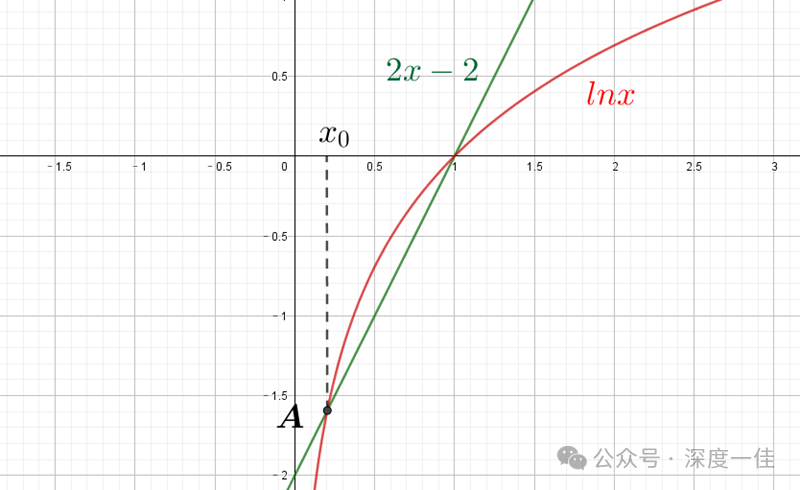
二者除了在（1,0）相交之外，还有另外一个交点A，对应极值点为x₀,A点之前，绿上红下，导函数大于0，原函数递增；A点和（1,0）点之间，红上绿下，导函数小于0，原函数递减；（1,0）点之后，导函数又大于0，原函数估计就是一路狂飙了。

原来如彼！

不过，图像上的A点虽然非常明确，但我们必须用数理的办法证明这个点的存在才行，否则，考卷上用数形结合的方法得出结论是会被判定不严谨的。

那么如何证明A点的存在呢？

我们只能对导函数的单调性做些研究：

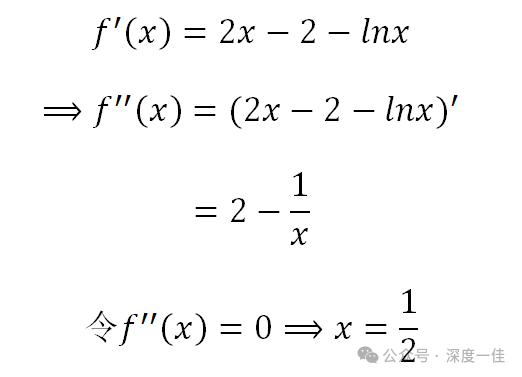
二阶导告诉我们，导函数在（0,1/2）之间是单调递减的，1/2后单调增，在1/2处获得最小值：

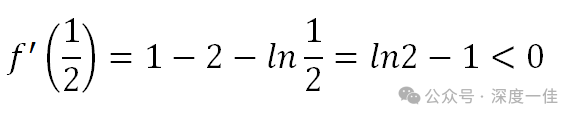
最小值小于0，

在x=1/2右侧：

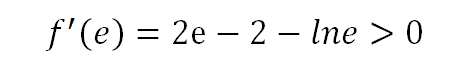
在x=1/2左侧

也就是说，在（0,1/2）之间，导函数存在唯一零点,而且，这个零点的大致范围是：

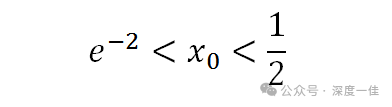
用代数语言表示：

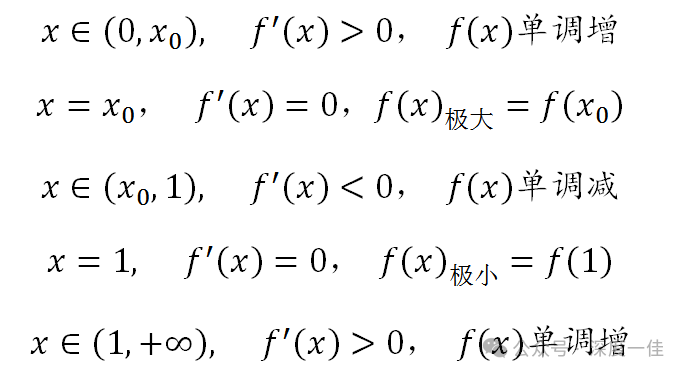
原函数定义域为开区间，端点值开放，两端不存在极值，So，

f(x₀)为原函数唯一极大值，x₀为函数唯一极大值点。

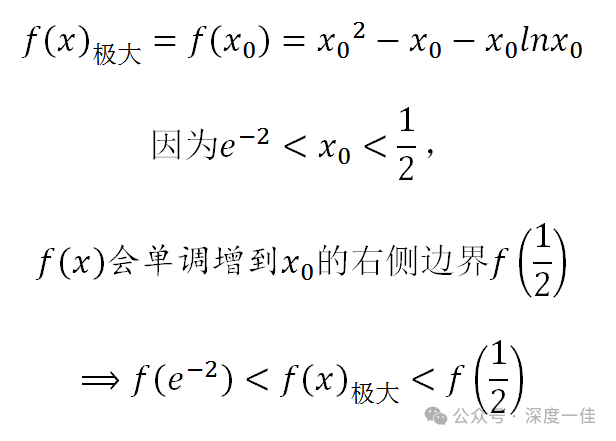
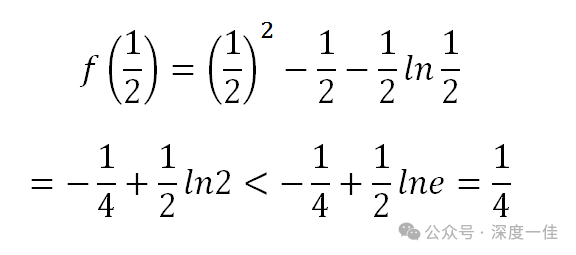
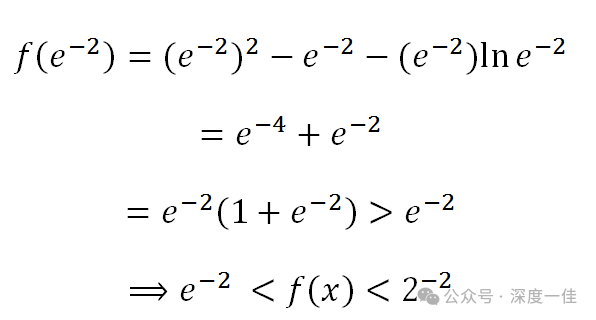
函数极大值范围由此得证。