几何常见辅助线口诀

三角形

图中有角平分线，可向两边作垂线

也可将图对折看，对称以后关系现

角平分线平行线，等腰三角形来添

角平分线加垂线，三线合一试试看

线段垂直平分线，常向两端把线连

线段和差及倍半，延长缩短可试验

线段和差不等式，移到同一三角去

三角形中两中点，连接则成中位线

三角形中有中线，倍长中线得全等

四边形

平行四边形出现，对称中心等分点

梯形问题巧转换，变为三角或平四

平移腰，移对角，两腰延长作出高

如果出现腰中点，细心连上中位线

上述方法不奏效，过腰中点全等造

证相似，比线段，添线平行成习惯

等积式子比例换，寻找线段很关键

直接证明有困难，等量代换少麻烦

斜边上面作高线，比例中项一大片

圆形

半径与弦长计算，弦心距来中间站

圆上若有一切线，切点圆心半径连

切线长度的计算，勾股定理最方便

要想证明是切线，半径垂线仔细辨

是直径，成半圆，想成直角径连弦

弧有中点圆心连，垂径定理要记全

圆周角边两条弦，直径和弦端点连

弦切角边切线弦，同弧对角等找完

要想作个外接圆，各边作出中垂线

还要作个内接圆，内角平分线梦圆

如果遇到相交圆，不要忘作公共弦

内外相切的两圆，经过切点公切线

若是添上连心线，切点肯定在上面

要作等角添个圆，证明题目少困难

由角平分线想到的辅助线

一、截取构全等

如图，AB//CD，BE平分∠ABC，CE平分∠BCD，点E在AD上，求证：BC=AB+CD。

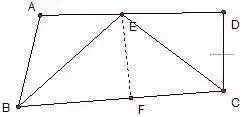
分析：在此题中可在长线段BC上截取BF=AB，再证明CF=CD，从而达到证明的目的。这里面用到了角平分线来构造全等三角形。另外一个全等自已证明。此题的证明也可以延长BE与CD的延长线交于一点来证明。自己试一试。

二、角分线上点向两边作垂线构全等

如图，已知AB>AD， ∠BAC=∠FAC，CD=BC。求证：∠ADC+∠B=180°。

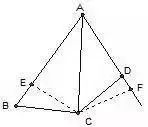
分析：可由C向∠BAD的两边作垂线。近而证∠ADC与∠B之和为平角。

三、三线合一构造等腰三角形

如图，AB=AC，∠BAC=90° ，BD为∠ABC的平分线，CE⊥BE。求证：BD=2CE。

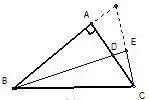
分析：延长此垂线与另外一边相交，得到等腰三角形，随后全等。

四、角平分线+平行线

如图，AB>AC, ∠1=∠2，求证：AB－AC>BD－CD。

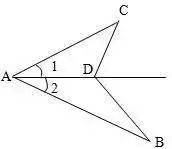
分析：在AB上截取AE=AC，通过全等和组成三角形的三边关系可证。

由线段和差想到的辅助线

截长补短法

AC平分∠BAD，CE⊥AB，且∠B+∠D=180°，求证：AE=AD+BE。

分析：过C点作AD垂线，得到全等即可。

由中点想到的辅助线

一、中线把三角形面积等分

如图，ΔABC中，AD是中线，延长AD到E，使DE=AD，DF是ΔDCE的中线。已知ΔABC的面积为2，求ΔCDF的面积。

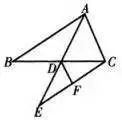
分析：利用中线平分三角形的面积求解。

二、中点联中点得中位线

如图，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，BA、CD的延长线分别交EF的延长线于点G、H。求证：∠BGE=∠CHE。

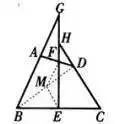
分析：取BD的中点M，连接ME、MF，通过中位线得平行传递角度。

三、倍长中线

如图，已知ΔABC中，AB=5，AC=3，连BC上的中线AD=2，求BC的长。

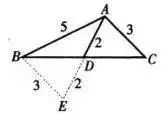
分析：倍长中线得到全等易得。

四、RTΔ斜边中线

如图，已知梯形ABCD中，AB//DC，AC⊥BC，AD⊥BD，求证：AC=BD。

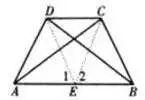
分析：取AB的中点E，得RTΔ斜边中线，得到等量关系。

由全等三角形想到的辅助线

一、倍长过中点得线段

已知，如图△ABC中，AB=5，AC=3，求中线AD的取值范围。

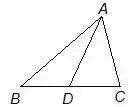
分析：利用倍长中线做。

二、截长补短

如图，在四边形ABCD中，BC＞BA,AD＝CD，BD平分∠ABC，求证：∠A+∠C=180°。

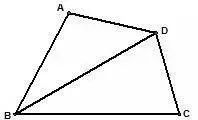
分析：在BC上截取BE=AB，通过全等求证。

三、平移变换

如图，在△ABC的边上取两点D、E，且BD=CE，求证：AB+AC>AD+AE。

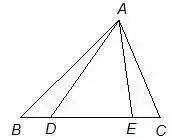
分析：将△ACE平移使EC与BD重合。

四、旋转

正方形ABCD中，E为BC上的一点，F为CD上的一点，BE+DF=EF，求∠EAF的度数。

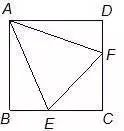
分析：将△ADF旋转使AD与AB重合。全等得证。

由梯形想到的辅助线

一、平移一腰

如图所示，在直角梯形ABCD中，∠A＝90°，AB∥DC，AD＝15，AB＝16，BC＝17. 求CD的长。

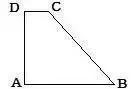
分析：利用平移一腰把梯形分割成三角形和平行四边形。

二、平移两腰

如图，在梯形ABCD中，AD//BC，∠B＋∠C=90°，AD=1，BC=3，E、F分别是AD、BC的中点，连接EF，求EF的长。

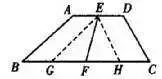
分析：利用平移两腰把梯形底角放在一个三角形内。

三、平移对角线

已知：梯形ABCD中，AD//BC，AD=1，BC=4，BD=3，AC=4，求梯形ABCD的面积。

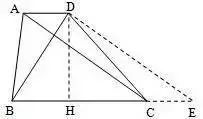
分析：通过平移梯形一对角线构造直角三角形求解。

四、作双高

在梯形ABCD中，AD为上底，AB>CD，求证：BD>AC。

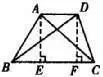
分析：作梯形双高利用勾股定理和三角形三边的关系可得。

五、作中位线

（1）如图，在梯形ABCD中，AD//BC，E、F分别是BD、AC的中点，求证：EF//AD。

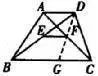
分析：连DF并延长，利用全等即得中位线。

（2）在梯形ABCD中，AD∥BC， ∠BAD=90°，E是DC上的中点，连接AE和BE，求证：∠AEB=2∠CBE。

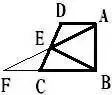
分析：在梯形中出现一腰上的中点时，过这点构造出两个全等的三角形达到解题的目的。