初中数学模型汇总

全等变换模型

平移：平行等线段（平行四边形）

对称：角平分线或垂直或半角

旋转：相邻等线段绕公共顶点旋转

对称全等模型：

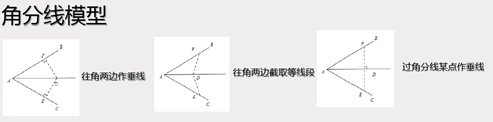
【说明】

以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。两边进行边或者角的等量代换，产生联系。垂直也可以做为轴进行对称全等。

对称半角模型：

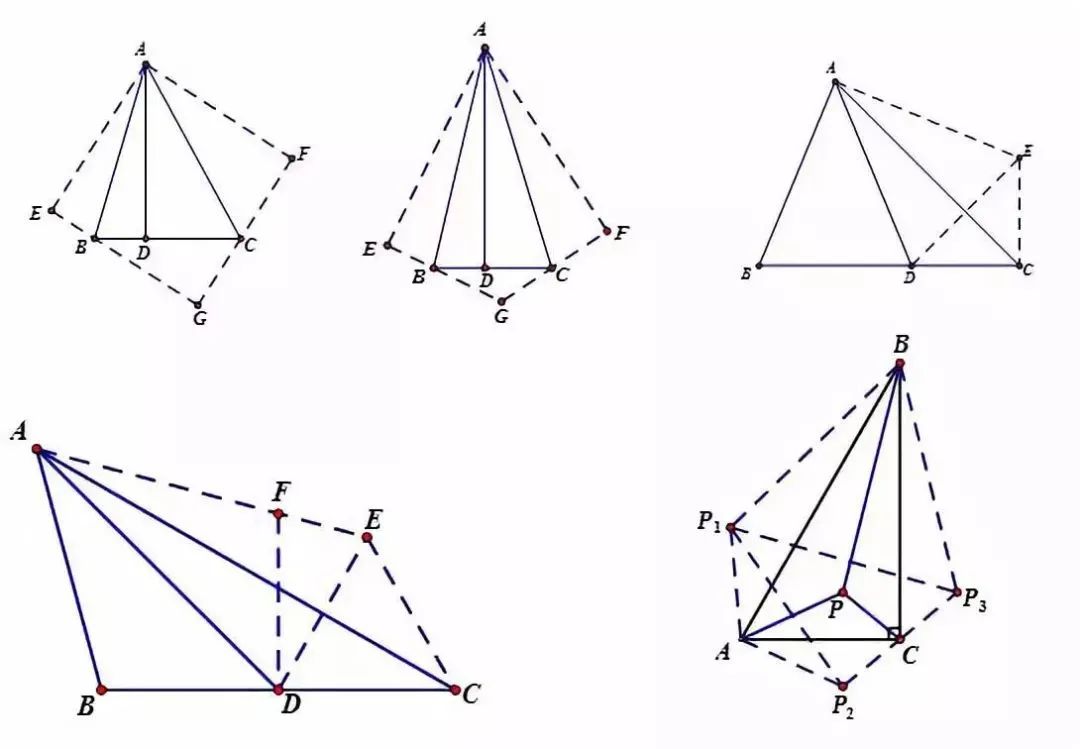
【说明】

上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型：

半角：有一个角含1/2角及相邻线段

自旋转：有一对相邻等线段，需要构造旋转全等

共旋转：有两对相邻等线段，直接寻找旋转全等

中点旋转：倍长中点相关线段转换成旋转全等问题

旋转半角模型：

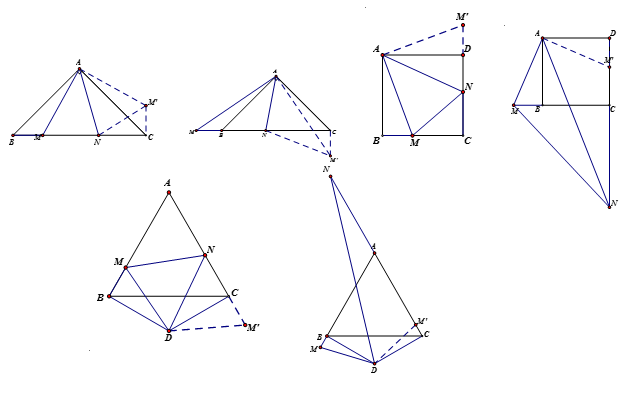
【说明】

旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

自旋转模型

构造方法：

遇60度旋60度，造等边三角形

遇90度旋90度，造等腰直角

遇等腰旋顶点，造旋转全等

遇中点旋180度，造中心对称

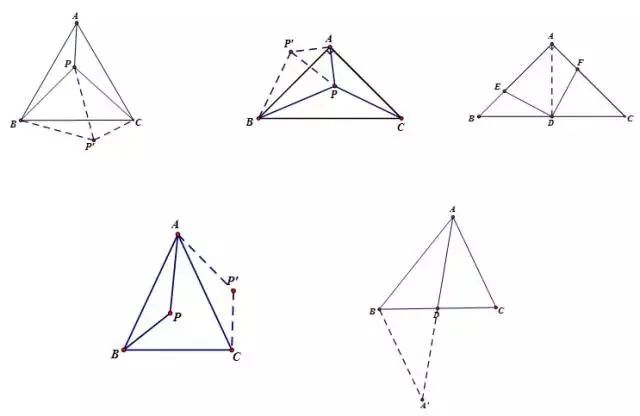
共旋转模型

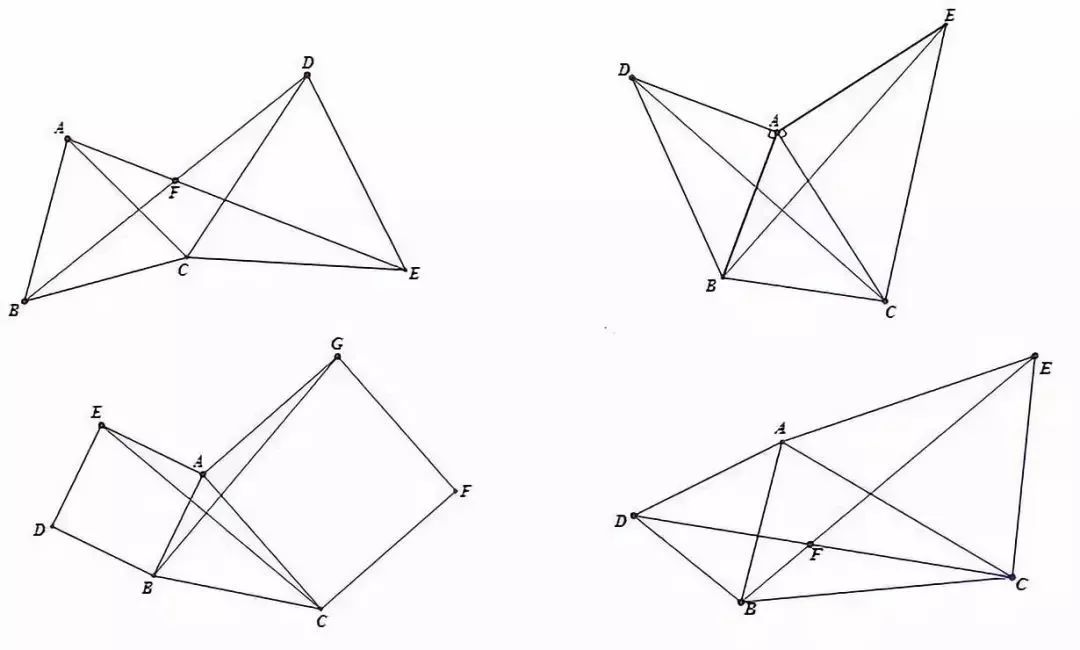
【说明】

旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。通过“8”字模型可以证明。

模型变形

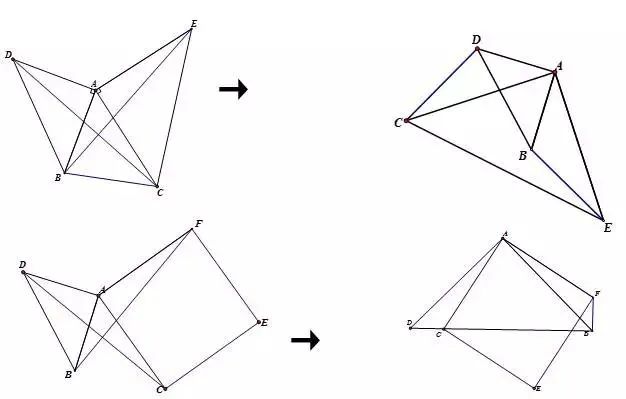
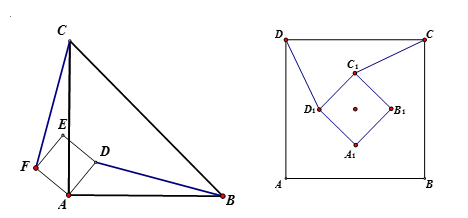
【说明】

模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

中点旋转：

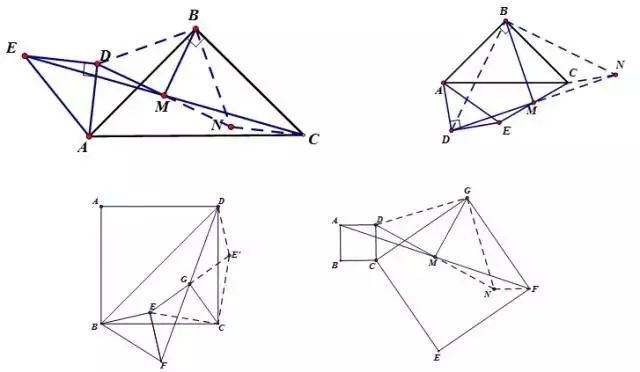
【说明】

两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点，证明另外两个顶点与中点所成图形为等腰直角三角形。

证明方法是倍长所要证等腰直角三角形的一直角边，转化成要证明的等腰直角三角形和已知的等腰直角三角形（或者正方形）公旋转顶点，通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

几何最值模型

对称最值(两点间线段最短)

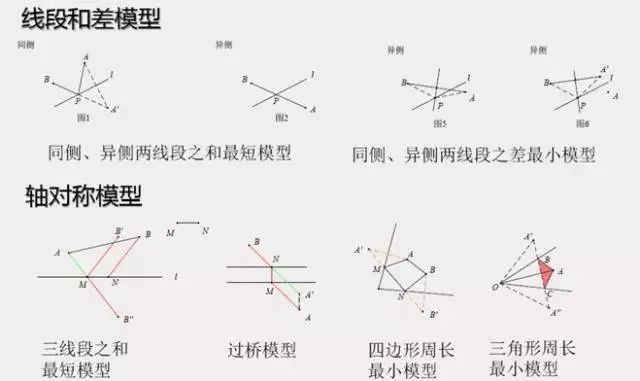
对称最值(点到直线垂线段最短)

【说明】

通过对称进行等量代换，转换成两点间距离及点到直线距离。

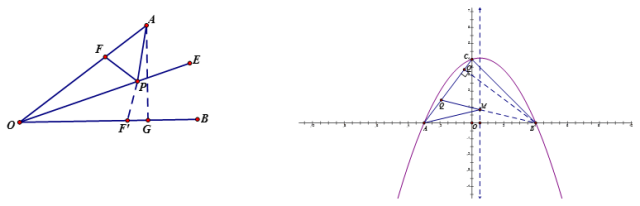
旋转最值(共线有最值)

【说明】

找到与所要求最值相关成三角形的两个定长线段，定长线段的和为最大值，定长线段的差为最小值。

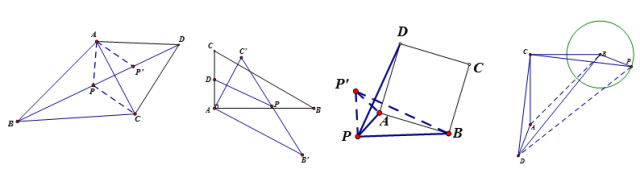
简拼模型

三角形→四边形

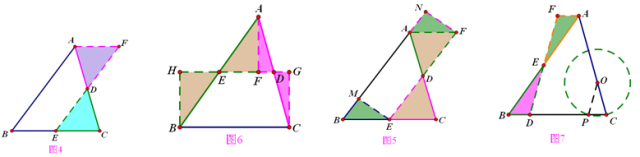
四边形→四边形

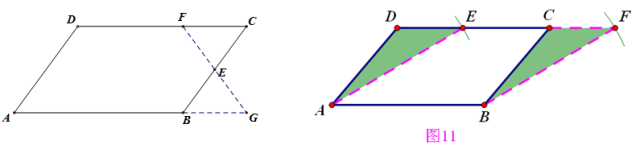
【说明】

剪拼主要是通过中点的180度旋转及平移改变图形的形状。

矩形→正方形

【说明】

通过射影定理找到正方形的边长，通过平移与旋转完成形状改变

正方形+等腰直角三角形→正方形

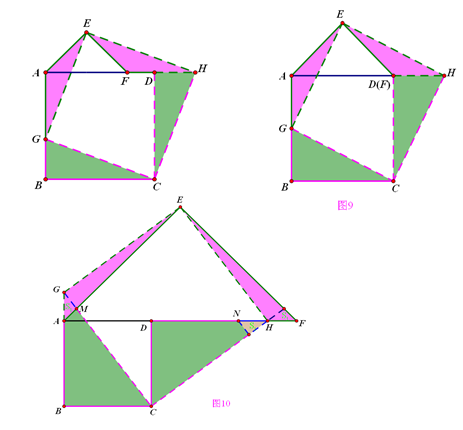
面积等分

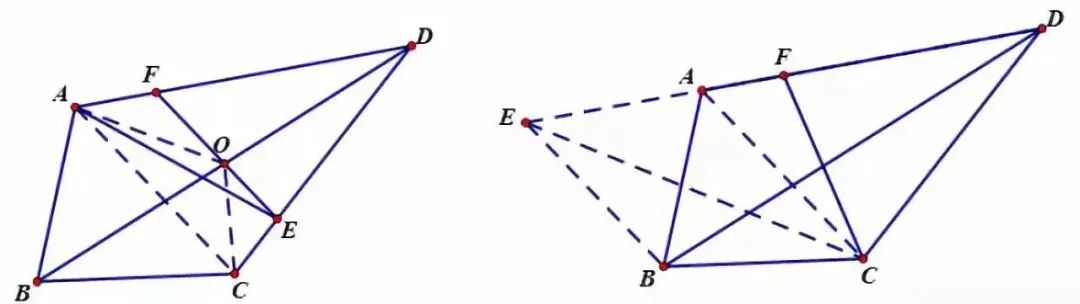
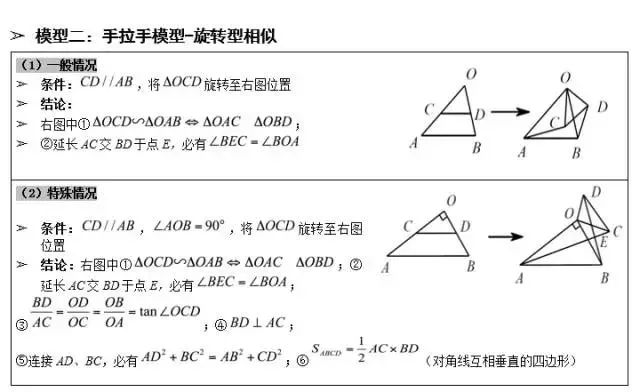
旋转相似模型

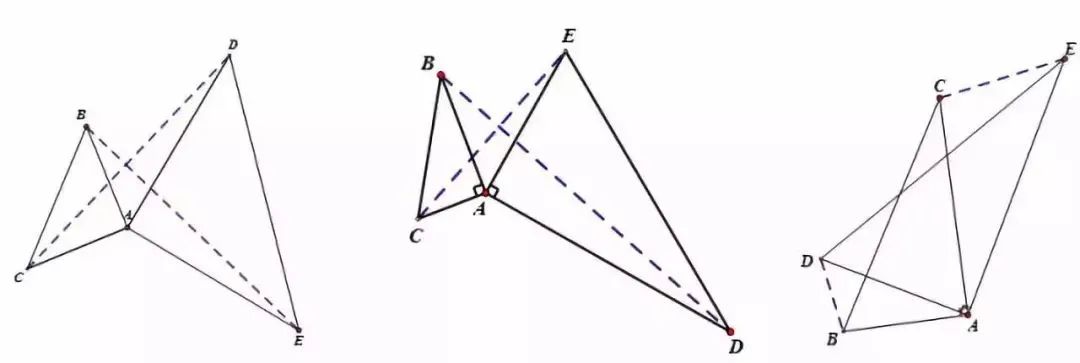
【说明】

两个等腰直角三角形成旋转全等，两个有一个角是300角的直角三角形成旋转相似。

推广：两个任意相似三角形旋转成一定角度，成旋转相似。第三边所成夹角符合旋转“8”字的规律。

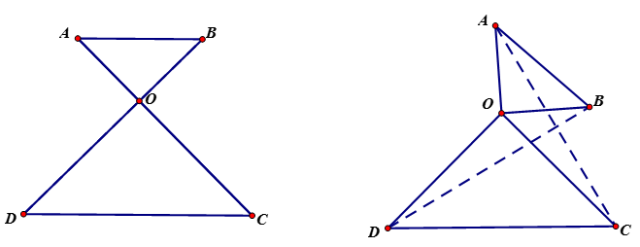
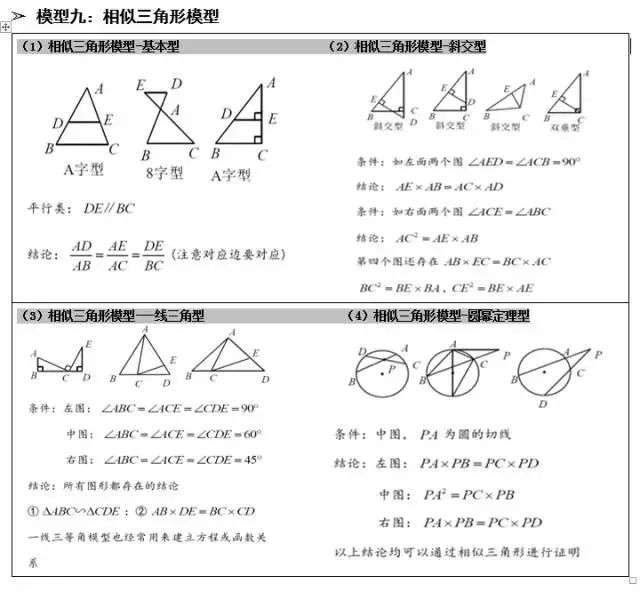
相似模型

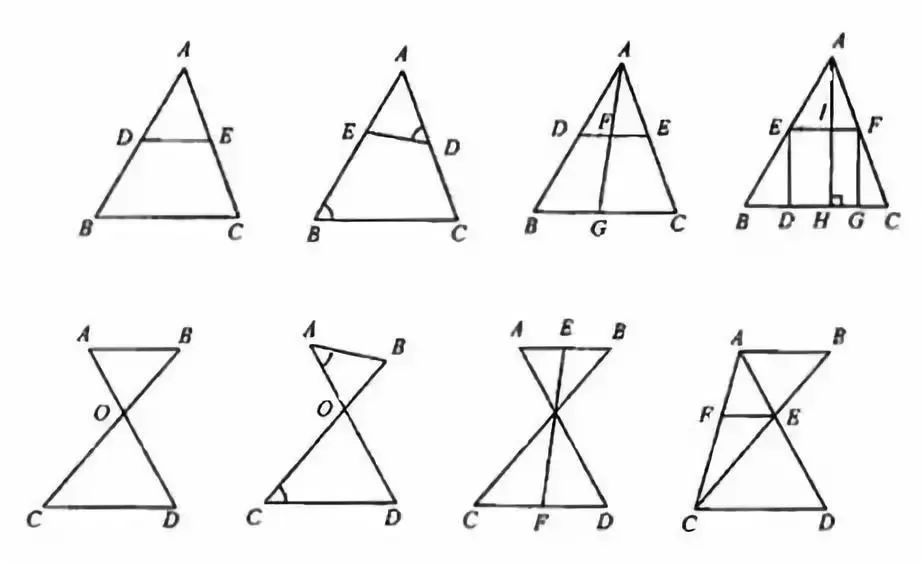
【说明】

注意边和角的对应，相等线段或者相等比值在证明相似中起到通过等量代换来构造相似三角形的作用。

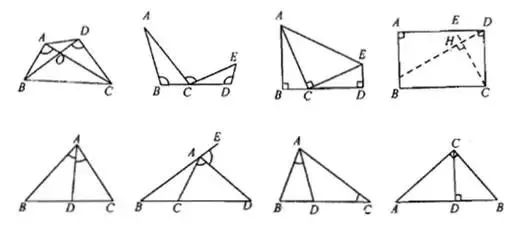
【说明】

（1）三垂直到一线三等角的演变，三等角以30度、45度、60度形式出现的居多。

（2）内外角平分线定理到射影定理的演变，注意之间的相同与不同之处。另外，相似、射影定理、相交弦定理（可以推广到圆幂定理）之间的比值可以转换成乘积，通过等线段、等比值、等乘积进行代换，进行证明得到需要的结论。

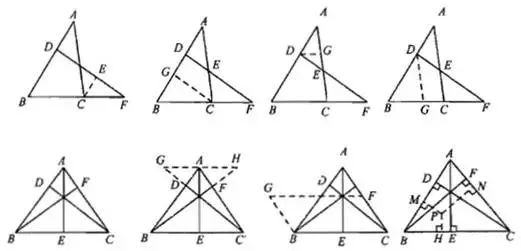
【说明】

相似证明中最常用的辅助线是做平行，根据题目的条件或者结论的比值来做相应的平行线。

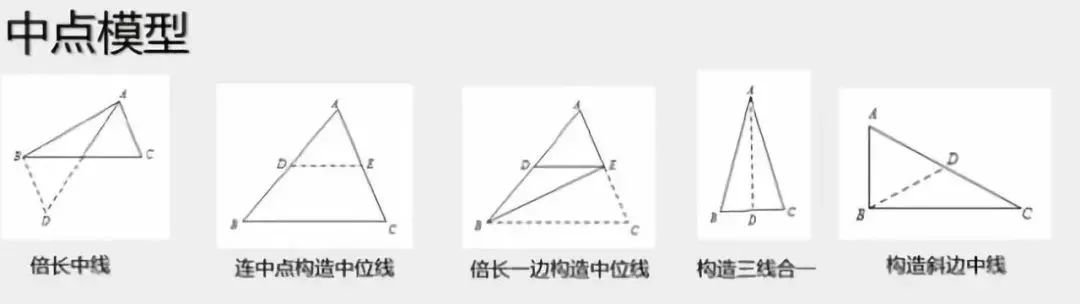
中点模型

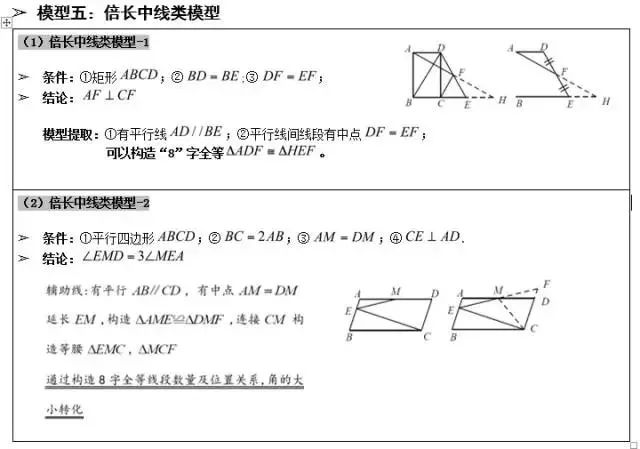
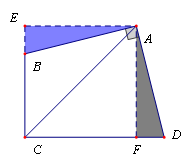
【模型1】倍长

1、 倍长中线；2、倍长类中线；3、中点遇平行延长相交

【模型2】遇多个中点，构造中位线

1、 直接连接中点；2、连对角线取中点再相连

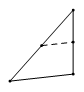
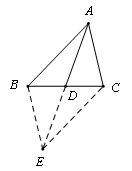
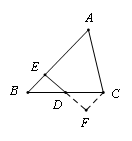
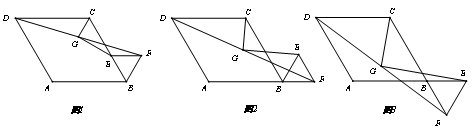
【例】在菱形ABCD和正三角形BEF中，∠ABC=60°，G是DF的中点，连接GC、GE．

（1）如图1，当点E在BC边上时，若AB=10，BF=4，求GE的长；

（2）如图2，当点F在AB的延长线上时，线段GC、GE有怎样的数量和位置关系，写出你的猜想；并给予证明；

（3）如图3，当点F在CB的延长线上时，(2)问中关系还成立吗？写出你的猜想，并给予证明.

角平分线模型

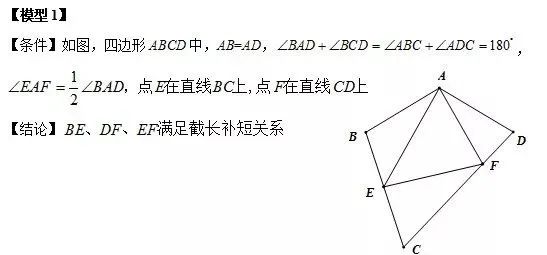
【模型1】构造轴对称

【模型2】角平分线遇平行构造等腰三角形

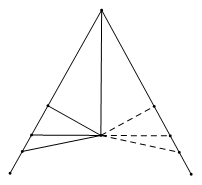
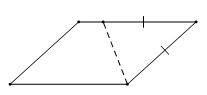
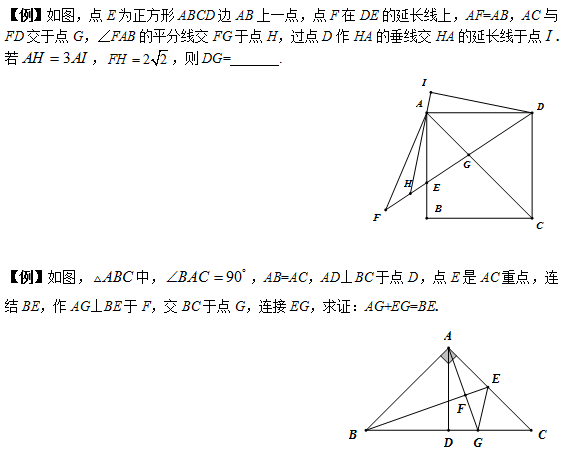
【例】如图，平行四边形ABCD中，AE平分∠BAD交BC边于E，EF⊥AE交CD边于F，交AD边于H，延长BA到点G，使AG=CF，连接GF．若BC=7，DF=3，EH=3AE，则GF的长为

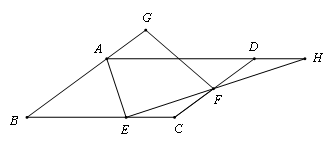
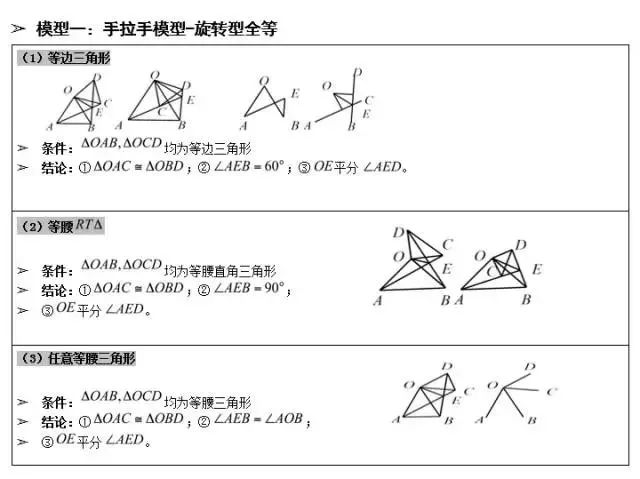
手拉手模型

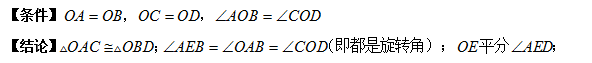
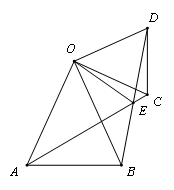
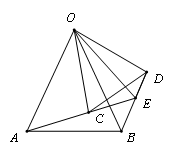
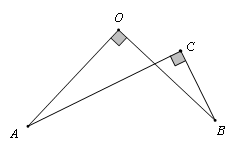
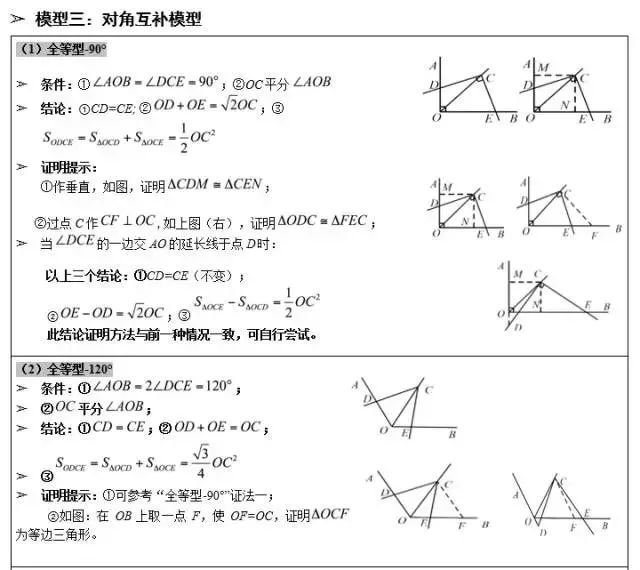
邻边相等的对角互补模型

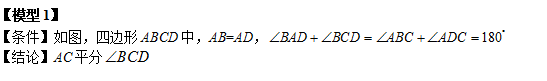
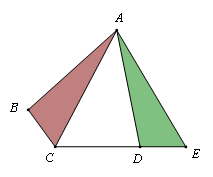
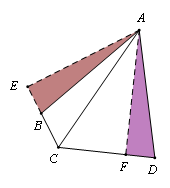
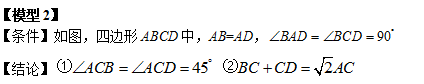
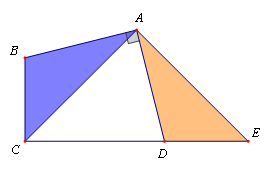
【例】如图，矩形ABCD中，AB=6，AD=5，G为CD中点，DE=DG，FG⊥BE于F，则DF 为

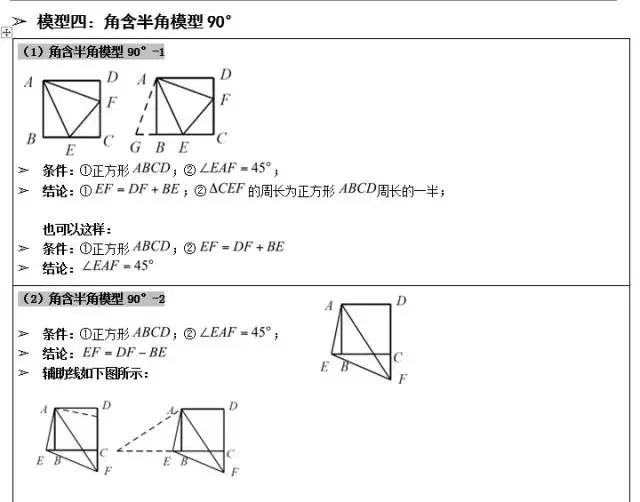
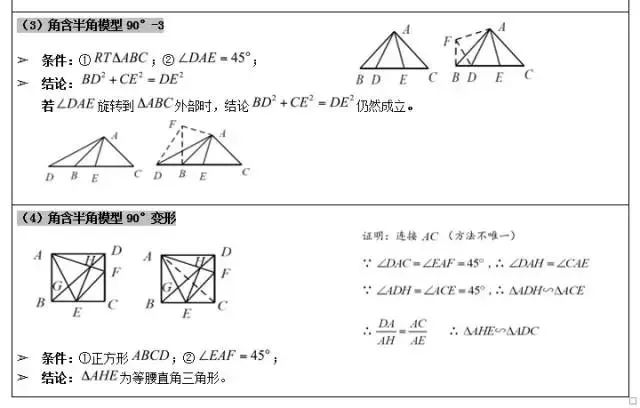
半角模型

弦图模型

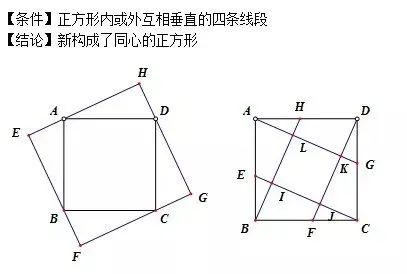
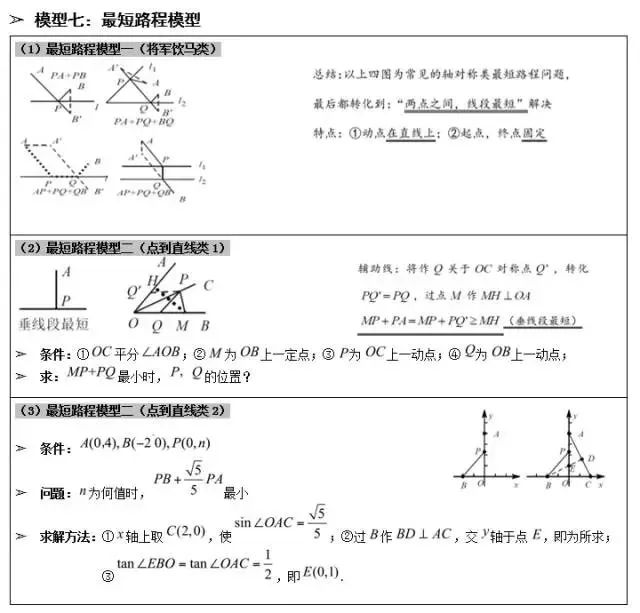
最短路径模型

【两点之间线段最短】

1、将军饮马

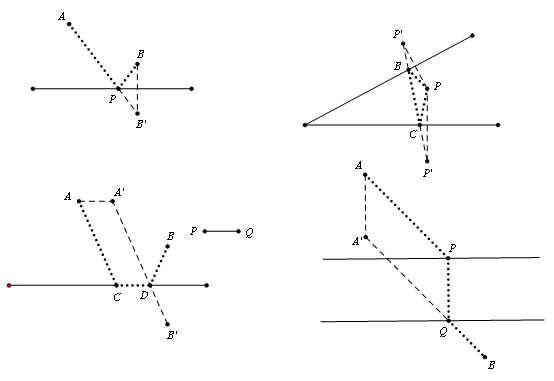
2、费马点

【垂线段最短】

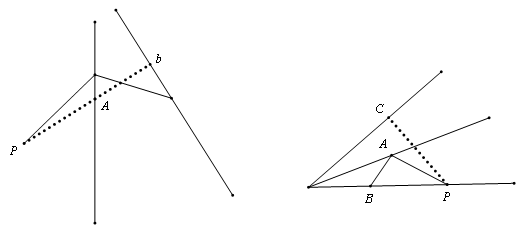
【两边之差小于第三边】

来源：网络，版权归原作者所有，如有侵权联系删除。