数学不在乎什么是显而易见的，它只想知道什么是真的
人类认知的历史中布满了言之凿凿的观点，这些观点在一段时间内被认为是真的，而后又被纠正或否认：我们曾认为太阳绕着地球转，还曾以为几何图形只有三种维度。我们自己的大脑可能会背叛我们，而最伟大的学者也曾犯下错误。
诚然，科学已经教会我们很多关于世界的知识，但它也应该让我们变得谦卑和心存怀疑。
译者：欧瑜
摘自《数学的雨伞下：理解世界的乐趣》
01
数学史上的转折点
公元前 5 世纪，一位名叫希波克拉底的数学家决定通过解决几何基础的问题来消除怀疑。他开始撰写《几何原本》，一部对几何领域已知成果进行了概括和统筹的著作。这本书立意高远：组织几何知识，并让这些知识立于无可辩驳的基础之上。这本书中不应含有任何轻率得出的论断，它所陈述的每一个定理都应该经过严谨而准确的证实。
希波克拉底的这本书未能留传下来。在随后的两个世纪中，紧随其后的学者们的著作也没能留传下来。所有这些成就都将在公元前 3世纪黯然失色，因为一个追随希波克拉底脚步的人完成了一部最完整、最成功的著作，那就是欧几里得。欧几里得洋洋十三卷的《几何原本》囊括了有关平面几何、算术、比例的问题，最后三卷则述及三维几何的问题。所有的内容都进行了系统的分类，从最简单的特性到最复杂的定理，还有对它们的完整论证。
欧几里得的《几何原本》标志着数学史上的转折点。当然，在《几何原本》问世之后，很多学者都发表过对其进行修订、扩充或评述后的版本。在随后的几个世纪中，书中的一些细节又几经讨论。但是，欧几里得定下的总体结构却从未受到过争议。
数学似乎在那以后步入了正确的轨道，并拥有了坚实而可靠的基石。有了《几何原本》，数学家们可以对自己所说的话确信无疑了。
但是，如果故事就此结束，那就太过简单了。因为《几何原本》的核心之处将孕育出一个全新类型的问题，而此前的任何文明都不曾遭遇过这个问题。一个关于数学本质的问题：第五公设。
02
最初的知识源于何处？
第五公设是科学史上的一座丰碑。尽管这样的评价始终带有主观性，但我个人斗胆称其为有史以来最大的数学谜题。这个谜题既核心又独特。它的影响是巨大的，而其陈述和解决办法的新颖之处使它成为一个数学神话。想要理解它，我们就必须深入了解《几何原本》的结构。
欧几里得的这部著作之所以既独特又现代，不仅仅是因为其中包含的数学成果，更是因为这些成果得以确立的方法。所有定理都必须经过严谨的证明。因此，《几何原本》中的每一个论断都伴随着一个论证，后者基于已经证明的结果通过逻辑推理来确立前者的准确性。
但是，这种方法会面临一个阻碍：必须得从某个地方入手。如果说，所有的推理都必须基于之前已有的知识，那么我们最初的知识又该基于什么呢？作为开山之作的《几何原本》该如何对它的第一个命题进行论证呢？希波克拉底、欧几里得和思考过这个问题的希腊学者们都知道没有奇迹之法。以下这个问题是绕不过去的：我们不能从零开始。为了让数学的机器运转起来，我们不得不在没有证明的情况下接受初始的论断。
但是，我们可以确保这些被接受的命题足够基础且显而易见，以便让人能够相信，这些命题将成为理论的基石，成为我们建造整幢数学大厦的基础。这些基本的真理被称为“公理”或“公设”。
于是，在《几何原本》的第一卷中，欧几里得决定使用五个公设来构建平面几何（图 4.1）。
所有这些陈述都是合理的，似乎很难引发争议。以此为基础，欧几里得对至今仍在世界各地的学校中教授的一系列几何结果进行了演示。我们会在其中看到毕达哥拉斯定理（即勾股定理）和泰勒斯定理（即截线定理），或是任意三角形的内角之和等于 180度。所有这些都来自欧几里得的五个公设。
03
行走在优雅的数学大厦中
为了能够充分理解我们之前所说的内容，让我们对此稍加讨论。务必注意一点：除了这五个公设，欧几里得绝对没有在事先未经证明的情况下陈述任何其他的真理，即便这个真理完全是一目了然的。
就以正方形为例，这是一些四条边都相等且四个角都是直角的图形。我们都见过正方形，毫无疑问，构造这样的图形是没有问题的。但是，《几何原本》中的五个公设没有一个提及这种图形。因此，在使用正方形之前，欧几里得证明了它们的存在。
这就是《几何原本》第一卷中的命题46。欧几里得以一条线段为基础，逐步说明了如何以这条线段为边作正方形（图 4.2）。
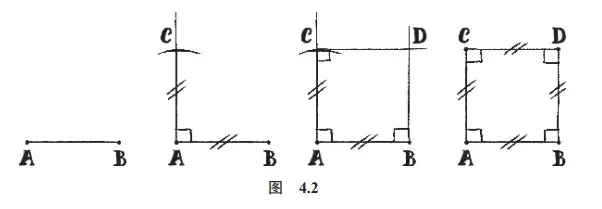
这种证明一切，乃至最基本之物的偏执，在欧几里得的追随者们看来，会招来某些哲学家，尤其是伊壁鸠鲁派的嘲笑。
对于后者来说，想要证明显而易见之事和不经讨论就去相信晦涩之事一样荒谬。比如第一卷中的命题 20。这一命题断言，从 A 点到 B 点，沿直线走要比经过不在直线 AB上的第三点 C 距离更短 A。如果驴位于 A 点，干草垛位于 B 点，那么驴会自然而然地沿直线走向干草垛，它不会想要经过 C点走过去（图 4.3）。
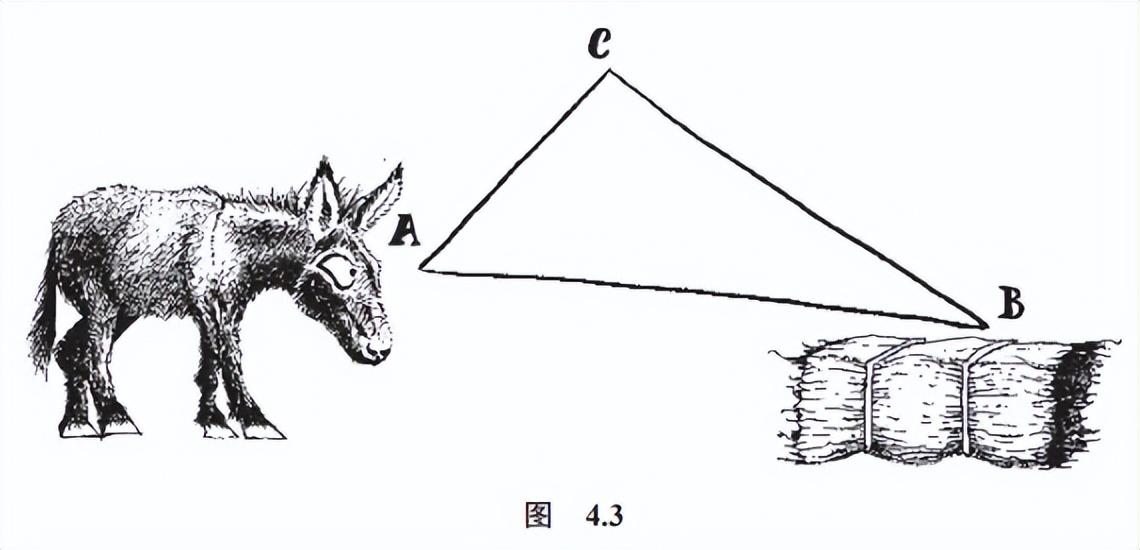
在伊壁鸠鲁派看来，欧几里得假意无视连驴都知道的事情是在自欺欺人。为什么要费尽力气去证明那些显而易见的事情呢？我们完全可以承认正方形是存在的，承认最短的距离是直线距离。
这么说实际上就是增加了两个假设。此外，我们还可以在整体上重新审视《几何原本》，并把所有我们认为“显而易见”的命题添加到公设中。毕竟，这么做会更简洁，因为这会让同时省去所有这些陈述的证明成为可能。
这两种看待事物的方式各有各的道理，但我个人会站在欧几里得这一边。我不知道你是怎么想的，但一想到那么多不必要的公设，我就感到头皮发麻。
相反，我觉得仅凭五个基本真理就能证明最显而易见的事情是分外优雅的。知道我们的数学大厦建立在最少的公设之上，这是一件非常令人高兴的事，不是吗？
但不要对欧几里得的意图有所误会。欧几里得并没有声称每一位几何学家都必须依靠他的五个公设去证明所需的那个定理。相反，《几何原本》是完全开放的，它提供了一套妙不可言的工具，让你不必在每次使用这些工具的时候都得去考虑命题的真实性。如果你需要《几何原本》中某个经过证明的结果，那么这个结果就在那里，任你差遣。既然欧几里得已经证明了正方形的存在，那么就该彻底解决这个问题了。自那以后，这个问题已经得到了解决。
但在优雅这种非常主观的问题之外，这种方法还带来了另一个问题。如果每看到一个对我们来说显而易见的断言就添加一个公设，那么就会很难知道在何处打住。显而易见和复杂定理之间的界线可能是模糊的，而且可能对每个人而言都不一样。欧几里得的方法让我们免于把时间浪费在关于什么显而易见而什么不是的争论上。数学不在乎什么是显而易见的，它只想知道什么是真的。
推荐阅读
译者：欧瑜
法国数学学会“达朗贝尔奖”得主新作
数学，是理解世界本质与万物关联的工具
本文由网络发布，不代表千千择校网立场，转载联系作者并注明出处：https://www.qqzexiao.com/jcjy/1575.html
