高中物理的传送带模型分析,附应用举例
传送带问题难点形成的原因:
1、对于物体与传送带之间是否存在摩擦力、是滑动摩擦力还是静摩擦力、摩擦力的方向如何,等等,这些关于摩擦力的产生条件、方向的判断等基础知识模糊不清;
2、对于物体相对地面、相对传送带分别做什么样的运动,判断错误;
3、对于物体在传送带上运动过程中的能量转化情况考虑不全面,出现能量转化不守恒的错误过程。
一、传送带模型分析
情景 | 传送带类别 | 图示 | 滑块可能的运动情况 | 滑块受(摩擦)力分析 |
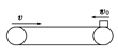
情景1 | 水平 |
| 一直加速 | 受力f=μmg |
先加速后匀速 | 先受力f=μmg,后f=0 | |||
情景2 | 水平 |
| v0>v,一直减速 | 受力f=μmg |
v0>v,先减速再匀速 | 先受力f=μmg,后f=0 | |||
v0<v,一直加速 | 受力f=μmg | |||
v0<v,先加速再匀速 | 先受力f=μmg,后f=0 | |||
情景3 | 水平 |
| 传送带长度l< | 受力f=μmg(方向一直向右) |
传送带长度l≥ | 受力f=μmg(方向一直向右) | |||
传送带长度l≥ | 减速和反向加速时受力f=μmg(方向一直向右),匀速运动f=0 | |||
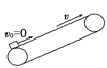
情景4 | 倾斜 |
| 一直加速 | 受摩擦力f=μmgcosθ |
先加速后匀速 | 先受摩擦力f=μmgcosθ,后f=mgsinθ | |||
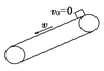
情景5 | 倾斜 |
| 一直加速 | 受摩擦力f=μmgcosθ |
先加速后匀速 | 先受摩擦力f=μmgcosθ,后f=mgsinθ | |||
先以加速度a1加速,后以加速度a2加速 | 先受摩擦力f=μmgcosθ,后受反向的摩擦力f=μmgcosθ | |||
情景6 | 倾斜 |
| 一直加速 | 受摩擦力f=μmgcosθ |
先加速后匀速 | 先受摩擦力f=μmgcosθ,后f=mgsinθ | |||
一直匀速(v0>v) | 受摩擦力f=mgsinθ | |||
一直匀速(v0=v) | 受摩擦力f=0 | |||
先以加速度a1加速,后以加速度a2加速 | 先受摩擦力f=μmgcosθ,后受反向的摩擦力f=μmgcosθ | |||
情景7 | 倾斜 |
| 一直加速 | 受摩擦力f=μmgcosθ |
一直匀速 | 受摩擦力f=mgsinθ | |||
先减速后反向加速 | 受摩擦力f=μmgcosθ |
倾斜的传送带
二、应用举例
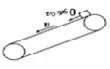
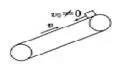
【例1】如图1所示,一水平传送装置由轮半径均为R=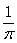 m的主动轮O1和从动轮O2及传送带等构成。两轮轴心相距8.0 m,轮与传送带不打滑。现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数为μ=0.4。(g取10 m/s2)求:
m的主动轮O1和从动轮O2及传送带等构成。两轮轴心相距8.0 m,轮与传送带不打滑。现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数为μ=0.4。(g取10 m/s2)求:
(1)当传送带以4.0 m/s的速度匀速运动时,将这袋面粉由左端O2正上方的A点轻放在传送带上后(设面粉初速度近似为零),这袋面粉由A端运送到O1正上方的B端所用的时间为多少?
(2)要想尽快将面粉由A端送到B端,主动轮O1的转速至少应为多大?
【解析】设这袋面粉质量为m,其在与传送带产生相对滑动的过程中所受摩擦力f=μmg。故其加速度为a=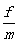 =μg=4.0 m/s2。
=μg=4.0 m/s2。
(1)若传送带的速度v带=4.0 m/s,则这袋面粉加速运动的时间t1=v带/a=1.0 s,在t1时间内的位移x1为x1= at12=2.0 m。
at12=2.0 m。
其后以v=4.0 m/s的速度做匀速运动,
x2=lAB-x1=vt2,
解得:t2=1.5 s。
运动的总时间为:t=t1+t2=2.5 s。
(2)要想时间最短,这袋面粉应一直向B端做加速运动,由lAB= at′2可得t′=2.0 s。
at′2可得t′=2.0 s。
面粉到达B端时的速度v′=at′=8.0 m/s,即传送带运转的最小速度。
由v′=ωR=2πnR可得:n=4 r/s=240 r/min。
水平传送带
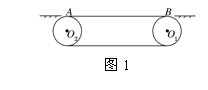
【例2】如图2所示,质量为m的物体从离传送带高为H处沿光滑圆弧轨道下滑,水平滑上长为L的静止的传送带并落在水平地面的Q点,已知物体与传送带间的动摩擦因数为μ,则当传送带转动时,物体仍以上述方式滑下,将落在Q点的左边还是右边?

【解析】物体从P点滑下,设水平滑上传送带时的速度为v0,则由机械能守恒mgH= mv02,可得
mv02,可得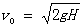 。
。
当传送带静止时,分析物体在传送带上的受力知物体做匀减速运动,a=μmg/m=μg。
物体离开传送带时的速度为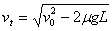 ,
,
随后做平抛运动而落在Q点。
当传送带逆时针方向转动时,分析物体在传送带上的受力情况与传送带静止时相同,因而物体离开传送带时的速度仍为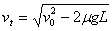 ,随后做平抛运动而仍落在Q点。
,随后做平抛运动而仍落在Q点。
(当v02<2μgL时,物体将不能滑出传送带而被传送带送回,显然不符合题意)
当传送带顺时针转动时,可能出现五种情况:
(1)当传送带的速度v较小,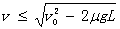 时,分析物体在传送带上的受力可知,物体一直做匀减速运动,离开传送带时的速度为
时,分析物体在传送带上的受力可知,物体一直做匀减速运动,离开传送带时的速度为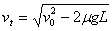 ,因而仍将落在Q点。
,因而仍将落在Q点。
(2)当传送带的速度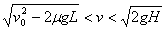 时,分析物体在传送带上的受力可知,物体将在传送带上先做匀减速运动,后做匀速运动,离开传送带时的速度
时,分析物体在传送带上的受力可知,物体将在传送带上先做匀减速运动,后做匀速运动,离开传送带时的速度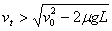 ,因而将落在Q点的右边。
,因而将落在Q点的右边。
(3)当传送带的速度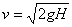 =v0时,则物体在传送带上不受摩擦力的作用而做匀速运动,离开传送带时的速度
=v0时,则物体在传送带上不受摩擦力的作用而做匀速运动,离开传送带时的速度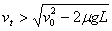 ,因而将落在Q点的右边。
,因而将落在Q点的右边。
(4)当传送带的速度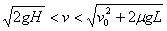 时,分析物体在传送带上的受力可知,物体将在传送带上先做匀加速运动,后做匀速运动,离开传送带时的速度
时,分析物体在传送带上的受力可知,物体将在传送带上先做匀加速运动,后做匀速运动,离开传送带时的速度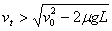 ,因而将落在Q点的右边。
,因而将落在Q点的右边。
(5)当传送带的速度v较大 时,分析物体在传送带上的受力可知,物体一直做匀加速运动,离开传送带时的速度为
时,分析物体在传送带上的受力可知,物体一直做匀加速运动,离开传送带时的速度为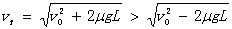 ,因而将落在Q点的右边。
,因而将落在Q点的右边。
综上所述:
当传送带逆时针转动或顺时针转动且速度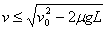 时,物体仍将落在Q点;
时,物体仍将落在Q点;
当传送带顺时针转动且速度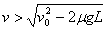 时,物体将落在Q点的右边。
时,物体将落在Q点的右边。
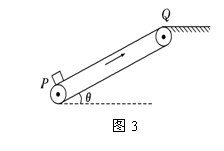
【例3】如图3所示,绷紧的传送带,始终以2 m/s的速度匀速斜向上运行,传送带与水平方向间的夹角θ=30°。现把质量为10 kg的工件轻轻地放在传送带底端P处,由传送带传送至顶端Q处。已知P、Q之间的距离为4 m,工件与传送带间的动摩擦因数为μ=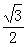 ,取g=10 m/s2。求:
,取g=10 m/s2。求:
(1)通过计算说明工件在传送带上做什么运动;
(2)求工件从P点运动到Q点所用的时间。
【解析】(1)对工件进行受力分析,由牛顿第二定律得:
μmgcosθ-mgsinθ=ma,
代入数值得:a=2.5 m/s2。
则其速度达到传送带速度时发生的位移为x1=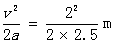 =0.8 m<4 m。
=0.8 m<4 m。
可见工件先匀加速运动0.8 m,然后匀速运动3.2 m。
(2)匀加速时,由x1=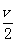 t1得t1=0.8 s,
t1得t1=0.8 s,
匀速上升时t2=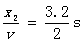 =1.6 s,
=1.6 s,
所以工件从P点运动到Q点所用的时间为t=t1+t2=2.4 s。
【例4】如图4所示,传送带与水平面夹角为37°,并以v=10m/s运行,在传送带的A端轻轻放一个小物体,物体与传送带之间的动摩擦因数μ=0.5,AB长16 m,求:以下两种情况下物体从A到B所用的时间。
(1)传送带顺时针方向转动;
(2)传送带逆时针方向转动。
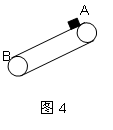
【解析】(1)传送带顺时针方向转动时受力如图4-1,由牛顿第二定律得
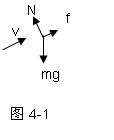
mgsinθ-μmgcosθ=ma,
物体下滑的加速度为a=gsinθ-μgcosθ=2m/s2。
加速的位移为s= at2,故有加速的时间为:
at2,故有加速的时间为: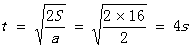 。
。
(2)传送带逆时针方向转动物体受力如图4-2,开始摩擦力方向向下,向下匀加速运动。
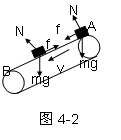
a=gsin37°+μgcos37°=10m/s2,
加速的时间为t1=v/a=1s。
加速的位移为s1= at2=5m,
at2=5m,
还剩位移s2=11m。
由题意,1s后,速度达到10m/s,摩擦力方向变为向上,由牛顿第二定律得
a2=g sin37°-μg cos37°=2 m/s2。
由运动学公式得s2=vt2+ a2t22,解得t2=1s,
a2t22,解得t2=1s,
故从A点到B点的时间为t=t1+t2=2s。
传送带问题如何入手?
三、题后反思
在水平方向的传送带问题中物块的受力主要是讨论滑动摩擦力,在存在相对运动时就会存在摩擦力,因此分析问题时以滑块是否与传送带共速为临界进行分析讨论。
在斜面方向上的传送带问题中物块的受力就要复杂些了,物体相对传送带滑动或者有滑动的趋势是判断摩擦力方向的关键,比如滑块受到沿斜面向下的滑动摩擦力作用,这样物体在沿斜面方向上所受的合力为重力的下滑分力和向下的滑动摩擦力,物体要做匀加速运动。
当物体加速到与传送带有相同速度时,摩擦力情况要发生变化,同速的瞬间可以看成二者间相对静止,无滑动摩擦力,但物体此时还受到重力的下滑分力作用,因此相对于传送带有向下的运动趋势。若重力的下滑分力大于物体和传送带之间的最大静摩擦力,此时有μ<tanθ,则物体将向下加速,所受摩擦力为沿斜面向上的滑动摩擦力;若重力的下滑分力小于或等于物体和传送带之间的最大静摩擦力,此时有μ≥tanθ,则物体将和传送带相对静止一起向下匀速运动,所受静摩擦力沿斜面向上,大小等于重力的下滑分力。
也可能出现的情况是传送带比较短,物体还没有加速到与传送带同速就已经滑到了底端,这样物体全过程都是受沿斜面向上的滑动摩擦力作用。
本文由千千择校网发布,不代表千千择校网立场,转载联系作者并注明出处:https://www.qqzexiao.com/gdjy/996.html

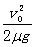

用户评论
终于有人总结了这个模型!我记得当时学习的时候非常费解,现在回头一看还是挺直观易懂的啊,特别是应用举例讲解的很到位!
有18位网友表示赞同!
这篇文章干货满满!物理竞赛准备需要用到这个模型,之前总是难以理解,看了你的分析和例子,感觉豁然开朗了。感谢分享!
有20位网友表示赞同!
高中物理教材真就喜欢整一些奇怪的词汇和模型嘛... 虽然说传送带模型确实能帮助理解某些物理现象,但还是希望老师能用更直观的语言解释啊...
有12位网友表示赞同!
这篇文章分析的太深入了,我不是学理科的,有点听不懂…不过可以看出来作者对这个模型很熟悉,讲解非常透彻,建议把一些关键概念解释得简单一些。
有18位网友表示赞同!
高中物理老师经常用这个模型来讲动量守恒,当时感觉很抽象,现在看了你的分析,终于明白了它的原理!还有应用举例真的很实用!
有12位网友表示赞同!
传送带模型确实可以用在很多场景中,举的例子也比较生动形象,我觉得这种学习方式更容易理解。建议以后再更新一些更复杂应用的情况,比如利用此模型解决三维问题等等。
有18位网友表示赞同!
虽然分析清晰,但感觉这个模型还是不够灵活,它只适用于特定的物理现象,遇到其他情况就用不了了。希望作者能提出更多不同的物理模型进行对比和分析。
有6位网友表示赞同!
这种方法真的太棒了!我之前一直都很困扰一些物理问题,现在看了你的分析,豁然开朗!
有18位网友表示赞同!
文章很好理解,应用举例也让我对这个理论有了更深入的认识。我觉得这篇文章很适合还在学习高中物理的学生参考。
有20位网友表示赞同!
虽然这个模型能够解释很多现象,但我还是觉得它有些过于简化了真实世界。现实中的物理问题往往更加复杂,难以用这样简单的模型来解决。
有16位网友表示赞同!
我一直不明白怎么用传送带模型计算动量,看了你的分析才终于明白!原来是这么个逻辑啊,真是受益匪浅!
有13位网友表示赞同!
文章写的不错,分析很到位,但应用举例中的一些例子显得过于简单化,缺乏实际操作中的复杂性。如果能再增加一些实战案例,效果会更佳!
有10位网友表示赞同!
传送带模型确实是个神奇的工具,可以帮助我们更好地理解物理现象背后的原理。作者的讲解非常清晰易懂,真是一位很棒的老师!
有11位网友表示赞同!
虽然这个模型能解释一部分现象,但我觉得现实中很多情况都更加复杂,不能简单地用这种模型来概括。我们需要更深入地研究物理背后真正运作的机制!
有6位网友表示赞同!
高中物理的时候就对这个模型一直没理解透彻,看了你的分析终于明白了其中的原理!非常感谢你的讲解!
有12位网友表示赞同!
这篇博客很有帮助,它将一个比较抽象的概念用通俗易懂的语言解释清楚了。 另外,应用举例也很生动形象,可以帮助我们更好地理解这个模型在实际中的运用。
有6位网友表示赞同!
虽然文章分析透彻,但如果能附一些图片或动画效果来辅助讲解,效果会更佳!因为有时候文字描述可能不够直观,视觉效果更容易让人理解复杂的概念。
有7位网友表示赞同!
传送带模型确实是一个好用的工具,但我建议作者将来可以讨论一下这个模型的局限性,以及在实践中该如何克服这些局限性を
有5位网友表示赞同!