【暑假伴学】高中 | 高中数学必修一~~必备知识点:21.二次函数的性质
第一章 集合与函数概念
二次函数
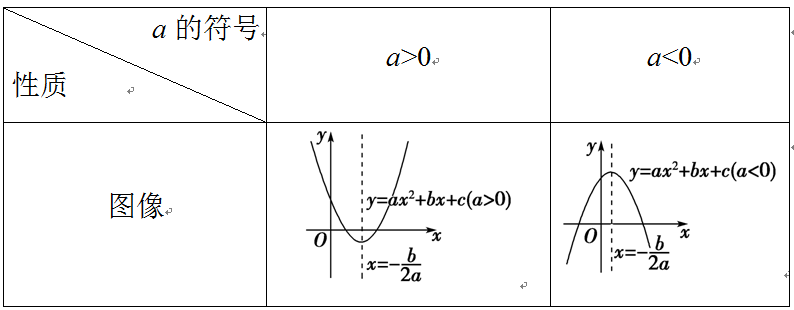
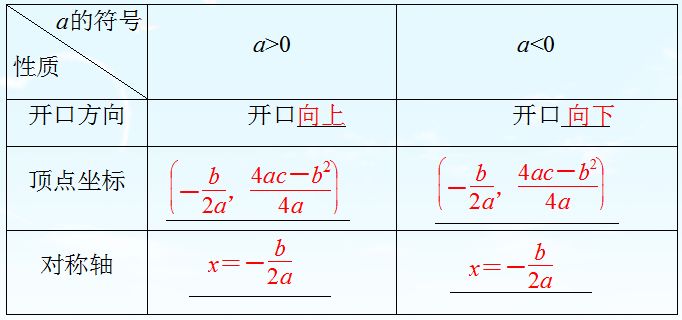
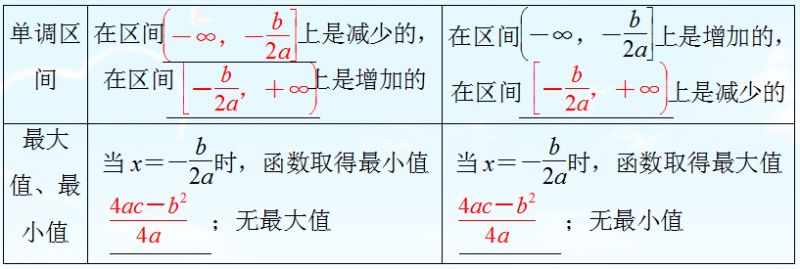
二次函数y=ax2+bx+c(a≠0)的性质
例题1:
已知函数y=f(x)=3x2+2x+1.
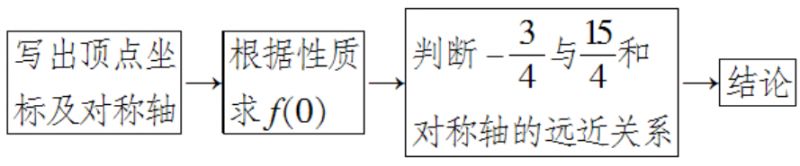
(1)求这个函数图像的顶点坐标和对称轴;
(2)已知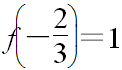 ,不计算函数值,求f(0);
,不计算函数值,求f(0);
(3)不直接计算函数值,试比较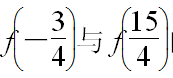 的大小.
的大小.
点拨:
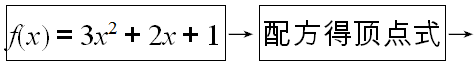
解:

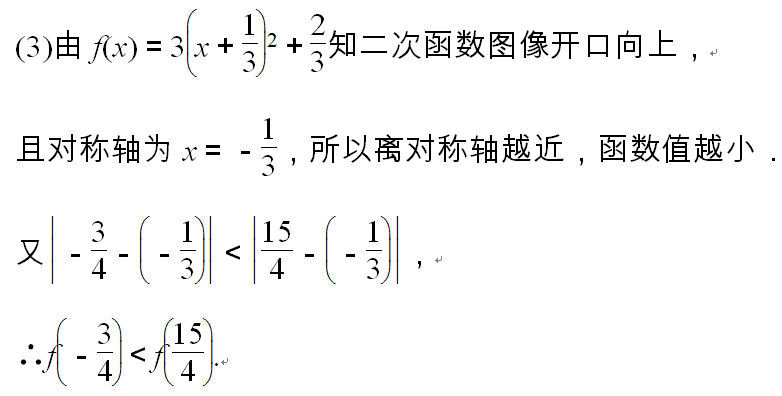
总结:
1.已知二次函数的解析式求顶点坐标及对称轴,一般先用配方法把二次函数解析式写成顶点式:y=a(x+h)2+k,进而确定顶点坐标为(-h,k),对称轴为x=-h.
2.比较两点函数值的大小,可以先比较两点离对称轴的距离大小,然后结合二次函数的开口方向,从而得到它们的大小关系,也可以将要比较的两个点转化到同一单调区间上,利用函数的单调性比较它们的大小.
练习:
1.已知二次函数f(x)=-x2+2ax,分别在下列条件下求实数a的取值(范围).
(1)f(x)在(-∞,2)上是增函数;
(2)f(x)的递增区间为(-∞,2).
【解】∵函数f(x)=-(x-a)2+a2的图像开口向下,对称轴为x=a,∴f(x)的单调递增区间为(-∞,a].
(1)由题意知(-∞,2)⊆(-∞,a],
∴a≥2,即实数a的取值范围是[2,+∞).
(2)由题意知,对称轴x=a=2,即实数a的取值为2.
例题2
某企业生产一种电器的固定成本(即固定投资)为0.5万元,每生产一台这种电器还需可变成本(即另增加投资)25元,市场对这种电器的年需求量为5百台.已知这种电器的销售收入(R)与销售量(t)的关系用抛物线段表示,如图2-4-2.
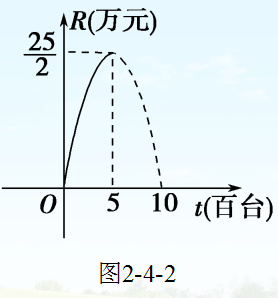
(年产量与销售量的单位:百台;纯收益的单位:万元,生产成本=固定成本+可变成本,精确到1台和0.01万元)
(1)写出如图的销售收入(R)与销售量(t)之间的函数关系R=f(t);
(2)认定销售收入减去生产成本为纯收益,写出纯收益与去年生产量的函数关系式,并求去年生产量是多少时纯收益最大.
点拨:
解答本题可先由图求出销售收入与销售量之间的函数关系式,即R=f(t),然后建立纯收益与销售量之间的函数关系式,进而求出纯收益的最大值.
解:

小结:
求解实际问题“四部曲”:读题:分为读懂和深刻理解两个层次,把“问题情景”译为数学语言,找出问题的主要关系(目标与条件的关系)。
(2)建模:把问题中的关系转化成函数关系,建立函数解析式,把实际问题转换成函数问题.
(3)求解:选择合适的数学方法求解函数.
(4)评价:对结果进行验证或评估,对错误加以改正,最后将结果应用于现实,做出解释或预测.也可认为分成“设元——列式——求解——作答”四个步骤
练习:
某工厂以x千克/小时的速度生产某种产品(生产条件要求1≤x≤10),每小时可获得的利润是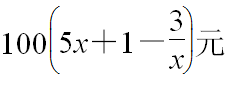 ,若生产该产品900千克,求该工厂获得的最大利润,以及此时的生产速度是多少?
,若生产该产品900千克,求该工厂获得的最大利润,以及此时的生产速度是多少?
解:

探究 1:
求二次函数f(x)=x2-2x+3在[-2,0]上的最值.
【提示】由f(x)=(x-1)2+2知抛物线开口向上,对称轴为x=1,
∴f(x)在[-2,0]上单调递减,
∴当x=-2时,f(x)有最大值f(-2)=11;
当x=0时,f(x)有最小值f(0)=3.
探究 2:
求探究1中函数f(x)在[-2,3]上的最值.
【提示】当x∈[-2,3]时,f(x)在[-2,3]上是先减后增的,故当x=1时,f(x)有最小值f(1)=2,
又|-2-1|>|3-1|,
∴f(x)的最大值为f(-2)=11.
例题3:
求探究1中函数f(x)在[t,t+1]的最小值g(t).
点拨:
可分析x=1与区间[t,t+1]的关系,就x=1是否落在区间[t,t+1]内展开讨论.


点拨:
求二次函数f(x)=ax2+bx+c(a>0)在[m,n]上的最值的步骤:
(1)配方,找对称轴.
(2)判断对称轴与区间的关系.
(3)求最值.若对称轴在区间外,则f(x)在[m,n]上单调,利用单调性求最值;
若对称轴在区间内,则在对称轴取得最小值,最大值在[m,n]端点处取得
练习:
求探究1中函数f(x)在[t,t+1]上的最大值h(t).
【解】①当t>1时,f(x)在[t,t+1]上单调递增,
所以当x=t+1时,f(x)取得最大值f(t+1)=(t+1)2-2(t+1)+3=t2+2.
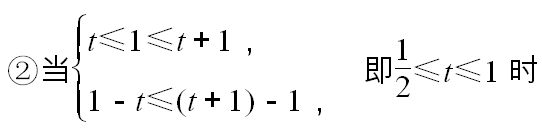 ,f(x)在[t,t+1]上先减后增,且对称轴更靠近于端点t,此时当x=t+1时,f(x)取得最大值
,f(x)在[t,t+1]上先减后增,且对称轴更靠近于端点t,此时当x=t+1时,f(x)取得最大值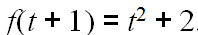
本文由千千择校网发布,不代表千千择校网立场,转载联系作者并注明出处:https://www.qqzexiao.com/gdjy/973.html


用户评论
我是高二的,明年准备复习这部分内容,正好看到这篇博文!讲解真清晰,特别是那些关于二次曲线形状和对称轴的解释,让我更容易理解了。感觉学习起来没那么可怕了!
有14位网友表示赞同!
暑假在家本来觉得没什么用处,结果没想到能学到这么多知识点啊!这次要好好掌握二次函数,因为期末考试还有不少用到这个内容的难题呢。
有15位网友表示赞同!
高中时我对数学一直苦手,二次函数更是令我头痛不已。看到这篇文章,感觉好像找到了解题的思路。下次做作业的时候试试看这种方法!希望我能真的搞懂二次函数!
有18位网友表示赞同!
对于我们学生来说,暑假不是放假休息时间吗?为什么还要把学习作为假期任务呢?虽然这篇博文讲解了很有用,但我觉得这只会让学生越来越焦虑。
有17位网友表示赞同!
这个知识点真是必不可少啊!我明年要去参加理科竞赛,感觉二次函数在几何图形上的应用会考到我。希望能在暑假前把这部分内容搞懂!
有8位网友表示赞同!
高中数学知识确实很多,尤其是那些抽象的概念。这篇博文解释特别细致,让我更容易理解二次函数的根、顶点、对称轴等等概念。学得真明白!
有17位网友表示赞同!
我觉得学习这些基础知识是很重要的,比如二次函数的性质。虽然现在看起来很枯燥,但未来一定会有用处。认真学习吧,同学们!
有14位网友表示赞同!
我是高中数学老师,给你们说的没错。暑假这段时间复习一下必修一的基础知识是很有必要的!这篇文章讲解得也很棒,可以作为学生们的参考教材。
有19位网友表示赞同!
每次考试都觉得二次函数是最难的,根本不知道怎么理解那些公式。希望这篇博文能帮到我在复习的时候
有18位网友表示赞同!
建议作者多讲一些实际应用中的例子,让大家更好的理解二次函数的意义!纯理论学习总感觉很空虚。
有6位网友表示赞同!
我明年考大学,数学是必修课啊!现在就开始把这个知识点搞好,希望可以帮助我更好地备考
有8位网友表示赞同!
这篇博文太酷了!我已经开始计划暑假如何复习二次函数的性质。感谢作者分享这么有用的资料!
有6位网友表示赞同!
我觉得这些高中的数学课程和考试内容都离学生的生活太远了,缺乏实际意义。学习的目标是为了解决问题,而不是为了考分。
有5位网友表示赞同!
为什么博文标题只有"高中 | 高中数学必修一~~"?难道不包含所有高中水平的知识吗?我觉得这篇文章更适合高二年级的学生学习。
有18位网友表示赞同!
暑假应该放松一下,好好休息!这些数学知识点,等学校开学再慢慢学不是更快吗?
有18位网友表示赞同!
虽然文章讲解得很透彻,但我还是觉得理解二次函数这种抽象的概念需要更多的练习和实践。希望作者可以提供一些实际案例,帮助我们更好地掌握。
有7位网友表示赞同!
感觉这篇博文对学习数学很有帮助!我想要学好数学,这篇文章一定可以成为我学习的指南针!
有11位网友表示赞同!