目录：

1. 《数学教学中的衔接问题-高等数学引桥》文章选登-无限—高等数学的第一坎

首先祝贺大家顺利过了高考关，即将成为新大学生！

这几天放飞一下，应该。

但是接下去，《高等数学》的坎正等着你们，不是我吓大家，有多少同学挂了科，其中不乏高考高分者。这是为什么？

原来高等数学和中学数学之间有很多不一样的地方。高中时，大多同学，拼命刷题，比较重视技巧，但高等数学，强调理解。这是一个很大的坎！

《高等数学引桥》可以祝你一臂之力。

这本书怎么样？----AI对《高等数学引桥》的看法

我对AI问了对《数学教学中的衔接问题-高等数学引桥》的看法。AI作了答复。总的来说，答案比较笼统。AI是这样说的：

《数学教学中的衔接问题-高等数学引桥》这本书是一部探讨数学教育中重要问题的著作。它专注于分析并解决高等数学教学中的衔接问题，旨在为学习者提供一个平稳的过渡，让他们能够顺利地从中学数学过渡到高等数学的学习。

这本书的特点在于深入浅出地讨论了数学概念的连续性和发展性。它不仅涵盖了一些基本的高等数学知识点，例如极限、导数、积分等，而且还对这些知识点进行了详细的解释和扩展，使得读者能够更好地理解这些概念的本质和应用。

此外，这本书还提供了一些实际的教学案例和练习题，帮助读者更好地应用所学的知识。这些案例和练习题的设计非常贴近实际教学，能够让读者在理论学习的同时，也能够锻炼自己的实际教学能力。

总的来说，我认为《数学教学中的衔接问题-高等数学引桥》是一本非常有价值的书籍，对于那些从事高等数学教育的工作者来说，它是一本不可或缺的参考书。无论是新手教师还是经验丰富的教师，都能从这本书中获得有用的信息和启示。

《数学教学中的衔接问题-高等数学引桥》文章选登

无限—高等数学的第一坎

微积分就是研究无限的，一开始就是数列的极限，后来是函数极限，函数的导数，积分，后来又回头研究级数，哪个场合都离不开无限。因为对同学来说，这是一种新的思想，所以，无限这个关不好过，好多同学直接就挂了。

涉及无限的疑虑、困惑、错误太多了。譬如极限可不可以达到？无穷小是不是数？无限项怎么可以求和？等等。因此过好无限关，是至关重要的。本文挑了几个有关无限的问题做点说明。希望能够帮助大家顺利过这个坎。

第一，务必理解有限项的“和”，以及无限项的“和”之间的区别。

例1 下列判断中正确的是（）

（A）0.9.=1 （B）0.9.<1

（C）0.9.≈1 （D）0.9.>1

这是出错率很高的一个问题。结果选（B）、（C）的占多数，其实正确答案是（A）。

很多人想不通，0.9.怎么会等于1呢？

首先要说明的是，这两个记号：

不都有省略号吗？有什么不同呢？

前者0.9999……的省略号在尾部，我们无法一一写出来，说明尾部有无限多个9，因此它是一个无限小数。而后者的省略号在中间。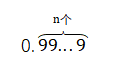包含很多个9，如10个9、100个9，甚至是n个9，因此它是一个有限小数，只是9的个数太多了，我们用省略号来表达。

也就是说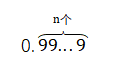，的省略号是为了方便而省略的，而0.9999……是因为根本写不完，所以只能用省略号表达。

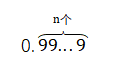可表示成有限和，而0.9999……表示成无限项的和。两者有本质的区别。

说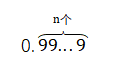<1是正确的，说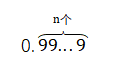≈1也对。但是，说

0.9999……<1

或0.9999……≈1，

就不对了。为什么呢？因为

0.9.=0.9999……=0.9+0.09+0.009+……，

这是一个无穷数列的“和”，它不再是小学里的“和”了，而是极限了！而根据无穷递缩等比数列的求和公式，它等于

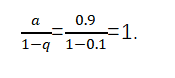
第二，要注意，有限和的性质不能随意搬到无限和的场合。

有限和有好几个运算性质，譬如加法交换律，结合律，分配率等等，但是这些性质在无限的场合，只有收敛的情形才成立，在发散的情形，或者在不知道收敛还是发散的时候，就不能想当然地迁移过来。

在一本以前的中师课本上有这么一段：

常有一些教参，出现一些“巧妙”的解法，如下例。

我们不知道此多重的无穷根式是不是等于一个数，即无限数列

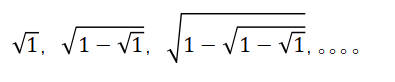
是不是有极限，因此设它等于A，一开始就缺少依据。接下去，有两边平方，这是有限情况下的一个性质，用到此处也没有依据。所以这个“巧妙”解法，并不正确。

第三，无限有好多种不同的无限。（略）

第四，求极限，套公式里有玄机。

微积分一上场，就会遇到求极限的题目。看起来只要套公式（极限运算法则），其实里面有些问题并不容易懂。

例：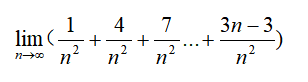

老师会告诉你：这个题不能不能直接利用和的极限运算法则进行分拆，即分拆成：

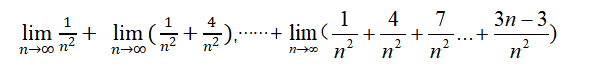
一定要先加，再用法则。为什么不能直接分拆？不是每个人都懂的。

首先看看我们在求怎样的一个数列的极限，我们具体写出数列各项：

随着项数增加，各项的小项数也在增加！也就是说，这个数列的各项排列起来是这样的：

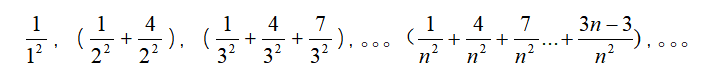
它的小项数目从1，2。。。以至无限，数列极限运算法则只能推广到有限项。因此不能直接运用极限运算法则，需要运用技巧---先求和。

这个例子是我听课时候遇到的，当时，和笔者一起听课的青年老师L轻轻地问我：

学生曾问她，“为什么无限项不能用法则？”她回答说：“无限项时误差积累太多了。”学生不理解，进一步问：“有限项的项数如果很多很多的话，误差也大的啊！”。L老师说，我回答不出来。

其实，有限项的和，还是加法的结果。而无限项的和，本质上已经不是加法的结果了，而是极限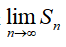,因此加法的性质（包括其他性质）不完全能够迁移到无限项的情形，（如果有限项时候的某个性质，在无限项时还是有的，必须重新证明）。因此有限项的极限运算法则不能随便套用到无限项的情形。

课后我回答了L老师，L老师很感慨地说：“看来我在误人子弟啊”。又说，“看来要让学生感悟解法的真正含义，否则，虽然用依样画葫芦的办法，做题目照样可以得高分，但实际上没有真懂。”

第五，不封闭的图形有时也可以有面积。(略)

第六，大数定律（略）

无穷引起的麻烦远不止这些，做好准备，我们不要再无穷中迷失方向！